Cálculo de Variância no Excel: Um Guia com Exemplos
A variância é uma medida estatística que nos diz o quão disperso está um conjunto de números. É um conceito crucial em finanças, ciência e muitos outros campos, ajudando-nos a entender a variabilidade ou dispersão dentro de nossos conjuntos de dados. O Excel oferece uma maneira direta de calcular a variância, tornando-a acessível tanto para iniciantes quanto para usuários avançados. Neste artigo, exploraremos como fazer isso com exemplos claros.
O que é variância?
Introdução às funções de variância no Excel
Como calcular a variância no Excel?
- VAR.S vs VAR.P – Calcular a variância a partir de uma amostra ou população
- VAR.S vs VARA – Calcular a variância incluindo ou excluindo textos e valores lógicos
Variância vs Desvio padrão
O que é variância?
A variância é um termo estatístico que descreve o grau em que os números em um conjunto de dados diferem da média, ou seja, da média dos números. Essencialmente, ela mede o quão dispersos estão os números. Um ponto-chave para entender a variância é reconhecer que ela quantifica o grau de variação ou dispersão dentro de um conjunto de valores. Uma alta variância indica que os números estão dispersos; uma baixa variância sugere que eles estão agrupados próximos à média.
Um Exemplo Simples para Ilustrar a Variância:
Cenário: Considere uma turma com cinco alunos e suas notas em um teste de matemática de 100 pontos. As notas são 90, 92, 88, 91 e 89.
Calcular a Média: Primeiro, encontramos a média (média) das notas. A média é
Calcular a Variância: Em seguida, calculamos a variância. Isso envolve subtrair a média de cada nota, elevar o resultado ao quadrado e depois calcular a média dessas diferenças ao quadrado.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
Um gráfico exibiu a distribuição das notas:
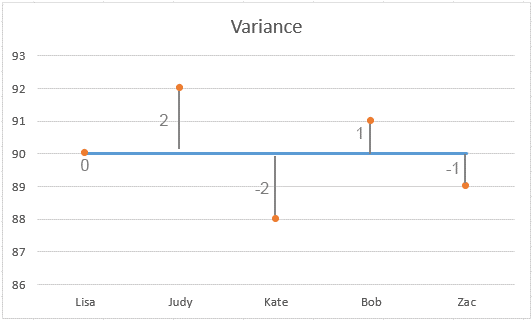
Compreendendo o Resultado:
Baixa Variância: Neste exemplo, a variância é 2. Isso é relativamente baixo, indicando que a maioria das notas está próxima da média (90). Quanto menor a variância, mais próximos os números individuais no conjunto estão da média.
Variância Zero: Se todos os alunos tivessem tirado exatamente 90, a variância seria 0, indicando nenhuma variabilidade. Todas as notas seriam iguais.
Alta Variância: Por outro lado, uma variância maior indicaria que as notas estão mais dispersas em relação à média, mostrando maior variabilidade no desempenho dos alunos.
Em resumo, a variância nos dá um valor numérico que ajuda a quantificar o quanto as notas (ou qualquer conjunto de números) se desviam do valor médio, fornecendo insights sobre a consistência ou variabilidade dos dados.
Introdução às funções de variância no Excel
O Excel fornece várias funções para calcular a variância, cada uma projetada para diferentes cenários de dados.
Compreender essas funções é crucial para uma análise estatística precisa
VAR.S (Variância Amostral, apenas incluindo números):
- Calcula a variância com base em uma amostra da população.
- Melhor usado ao analisar um subconjunto de dados para inferir sobre o todo.
VAR.P (Variância Populacional, apenas incluindo números):
- Calcula a variância para toda a população.
- Ideal quando você tem dados completos e não apenas uma amostra.
VARA (Variância Amostral, incluindo texto e lógicos):
- Semelhante ao VAR.S, mas inclui texto e valores lógicos no cálculo (texto é tratado como 0, VERDADEIRO como 1, FALSO como 0).
- Útil quando seu conjunto de dados contém tipos mistos (números, texto e valores lógicos).
VARPA (Variância Populacional, incluindo texto e lógicos):
- A versão de variância populacional do VARA.
- Inclui todos os tipos de dados no cálculo da variância para toda a população.
VAR (Variância Amostral Legado):
- Uma versão mais antiga do VAR.S, usada principalmente no Excel 2007 e anterior.
- Recomenda-se usar VAR.S nas versões mais recentes para consistência e clareza.
VARP (Variância Populacional Legado):
- A versão mais antiga do VAR.P.
- Assim como o VAR, recomenda-se usar VAR.P nas versões mais recentes do Excel.
Diferenças e Comparações:
- Amostra vs População: VAR.S e VARA são para amostras, enquanto VAR.P e VARPA são para toda a população.
- Consideração de Tipo de Dados: VARA e VARPA incluem texto e valores lógicos no cálculo, ao contrário de VAR.S e VAR.P.
- Funções Legadas vs Modernas: VAR e VARP são funções mais antigas e podem ser substituídas por VAR.S e VAR.P para melhor compatibilidade com as versões atuais do Excel.
Tabela de Comparação:
| Função | Tipo de Dados Considerados | População ou Amostra | Caso de Uso |
| VAR.S | Apenas Números | Amostra | Variância amostral para dados numéricos |
| VAR.P | Apenas Números | População | Variância populacional para números |
| VARA | Números, Texto, Lógicos | Amostra | Variância amostral para dados mistos |
| VARPA | Números, Texto, Lógicos | População | Variância populacional para dados mistos |
| VAR | Apenas Números | Amostra | Função legada para variância amostral |
| VARP | Apenas Números | População | Função legada para popular |

Desbloqueie a Magia do Excel com o Kutools AI
- Execução Inteligente: Realize operações de células, analise dados e crie gráficos — tudo impulsionado por comandos simples.
- Fórmulas Personalizadas: Gere fórmulas sob medida para otimizar seus fluxos de trabalho.
- Codificação VBA: Escreva e implemente código VBA sem esforço.
- Interpretação de Fórmulas: Compreenda fórmulas complexas com facilidade.
- Tradução de Texto: Supere barreiras linguísticas dentro de suas planilhas.
Como calcular a variância no Excel?
Nesta seção, forneceremos dois exemplos para demonstrar como calcular a variância no Excel e explicar as diferenças entre as várias funções de variância. Como resultado, você verá que diferentes funções de variância produzem resultados completamente diferentes para os mesmos dados de exemplo.
VAR.S vs VAR.P – Calcular a variância a partir de uma amostra ou população
Cenário: Calculando a variância para uma pequena amostra de uma população versus toda a população.
Exemplo: Calcule a variância para os valores na coluna A2:A12.
Fórmula: Selecione uma célula em branco e digite uma das fórmulas abaixo conforme necessário, depois pressione a tecla Enter.
Obtendo as variâncias para a amostra de um grande conjunto de dados (supondo que os valores em A2:A12 sejam partes de um grande conjunto de dados)
=VAR.S(A2:A12)
Obtendo a variância para toda a população (supondo que os valores em A2:A12 sejam o conjunto de dados completo)
=VAR.P(A2:A12)
Como você vê, os mesmos valores, mas usando diferentes funções de variância obterão resultados diferentes.
Por que os resultados de VAR.S e VAR.P são diferentes?
- VAR.S: Esta função é usada quando seu conjunto de dados representa uma amostra de uma população maior. Ela calcula a variância com base no método "n-1", onde "n" é o número de pontos de dados na amostra. Usar "n-1" em vez de "n" como denominador corrige o viés na amostra, tornando-a um estimador imparcial da variância populacional. Ela fornece uma estimativa de como os dados na amostra variam em torno da média da amostra.
- VAR.P: Esta função é usada quando seu conjunto de dados representa uma população inteira, não apenas uma amostra dela. Ela calcula a variância com base no método "n", onde "n" é o número de pontos de dados na população. Ela assume que o conjunto de dados cobre toda a população, então não há necessidade de corrigir o viés como em VAR.S.
- Em resumo, a principal diferença está no denominador da fórmula. VAR.S usa "n-1" para levar em conta a natureza amostral dos dados, enquanto VAR.P usa "n" para dados populacionais onde não há amostragem envolvida. Dependendo de seu conjunto de dados e se é uma amostra ou uma população completa, você deve escolher a função apropriada para calcular a variância.
VAR.S vs VARA – Calcular a variância incluindo ou excluindo textos e valores lógicos
Cenário: Decidindo se inclui valores lógicos e textos no cálculo da variância.
Exemplo: Calcule a variância para os valores na coluna A2:A12.
Fórmula: Selecione uma célula em branco e digite uma das fórmulas abaixo conforme necessário, depois pressione a tecla Enter.
Obtendo as variâncias para a amostra de um grande conjunto de dados ignorando textos e valores lógicos.
=VAR.S(A2:A12)
Obtendo a variância para a amostra de um grande conjunto de dados incluindo textos e valores lógicos.
=VARA(A2:A12)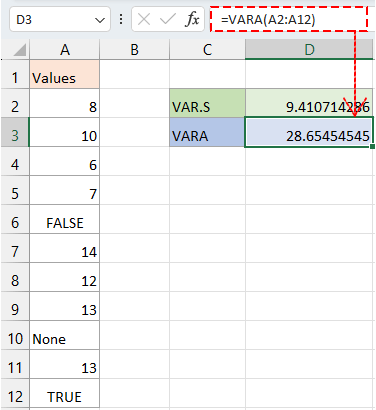
Faça Cálculos de Data e Hora Decolar
O Date Time Helper do Kutools para Excel é uma ferramenta incrivelmente eficiente projetada para simplificar cálculos complexos de data e hora. Experimente e veja como ele transforma sua experiência de gerenciamento de dados!
Variância vs Desvio Padrão
Similaridades:
Medida de Dispersão:
Tanto a variância quanto o desvio padrão são medidas estatísticas usadas para descrever a dispersão ou variação dentro de um conjunto de dados. Eles quantificam o quão longe os números individuais no conjunto se desviam da média (média).
Análise de Dados:
Ambos são comumente usados em análises estatísticas para entender a variabilidade dos dados. Eles são essenciais em áreas como finanças, pesquisa, controle de qualidade e muito mais.
Calculado a Partir da Média:
O cálculo tanto da variância quanto do desvio padrão começa com a média do conjunto de dados. Eles avaliam a variabilidade em relação a esse valor central.
Diferenças:
Unidades de Medida:
Variância: Unidades quadradas dos dados originais. Por exemplo, se os dados estiverem em metros, a variância será em metros quadrados.
Desvio Padrão: Mesmas unidades dos dados originais. Continuando o exemplo, se os dados estiverem em metros, o desvio padrão também estará em metros.
Interpretação:
Variância: Fornece uma estimativa quadrada que pode ser menos intuitiva de interpretar porque não está na mesma escala dos dados originais.
Desvio Padrão: Mais interpretável, pois está nas mesmas unidades dos dados. Ele indica a distância média dos pontos de dados em relação à média.
Definição Matemática:
Variância: A média das diferenças quadradas da Média.
Desvio Padrão: A raiz quadrada da variância.
Sensibilidade a Valores Extremos:
Variância: Mais sensível a valores extremos porque eleva as diferenças ao quadrado.
Desvio Padrão: Embora afetado por valores extremos, é menos sensível em comparação com a variância devido à raiz quadrada.
Aplicações:
Variância:
Usada quando o foco está na magnitude quadrada da dispersão.
Beneficiária em modelos e cálculos estatísticos onde o quadrado é necessário para anular valores negativos.
Muitas vezes usada em modelos financeiros para avaliação de risco, pois mede volatilidade.
Desvio Padrão:
Mais comumente usado em relatórios e aplicações diárias devido à sua relação direta com a escala dos dados.
Essencial em pesquisas empíricas para entender a variabilidade.
Frequentemente usado em controle de qualidade, previsões meteorológicas e escores padrão em testes.
Conclusão:
Embora a variância e o desvio padrão ambos sirvam para medir a dispersão de um conjunto de dados, suas aplicações diferem devido à sua unidade de medida e interpretabilidade. O desvio padrão, com sua relação direta com a escala dos dados, tende a ser mais amigável ao usuário, especialmente em contextos práticos e cotidianos. A variância, por outro lado, é frequentemente mais adequada para modelos matemáticos e estatísticos.
Esta visão geral e comparação devem fornecer uma compreensão clara de quando e por que usar cada função de variância no Excel, permitindo uma análise de dados mais precisa e significativa. Para mais estratégias revolucionárias no Excel que podem elevar seu gerenciamento de dados, explore mais aqui..
As Melhores Ferramentas de Produtividade para o Office
Kutools para Excel - Ajuda Você a Se Destacar na Multidão
O Kutools para Excel Oferece Mais de 300 Recursos, Garantindo que O Que Você Precisa Está Apenas a Um Clique de Distância...
Office Tab - Habilite a Leitura e Edição com Abas no Microsoft Office (inclui Excel)
- Um segundo para alternar entre dezenas de documentos abertos!
- Reduz centenas de cliques de mouse para você todos os dias, diga adeus à mão do mouse.
- Aumenta sua produtividade em 50% ao visualizar e editar vários documentos.
- Traz Guias Eficientes para o Office (inclui Excel), Assim Como Chrome, Edge e Firefox.
Índice
- O que é variância?
- Introdução às funções de variância no Excel
- Como calcular a variância no Excel?
- VAR.S vs VAR.P – Calcular a variância a partir de uma amostra ou população
- VAR.S vs VARA – Calcular a variância incluindo ou excluindo textos e valores lógicos
- Variância vs Desvio padrão
- Artigos Relacionados
- Melhores Ferramentas de Produtividade para o Office
- Comentários